9.2 Solutions
9.2.0.1 Exercise 1
- Load the non-western foreigners dataset (https://github.com/QMUL-SPIR/Public_files/raw/master/datasets/BSAS_manip.RData).
data2 <- readRDS(url("https://github.com/QMUL-SPIR/Public_files/raw/master/datasets/BSAS_manip.rds"))9.2.0.2 Exercise 2
Build a model that predicts over.estimate to find determinants of over-estimating the level of migration. Justify your choice of predictors and interpret the model output.
We include HHINC which measures levels of household income. Fears of migration are often assoicated with the ‘losers of globalization’ argument. Those who did not profit from globalization and are left behind oppose it. Furthermore, those who have lower incomes are more likely to have to compete with immigrants and, therefore, may be more opposed to it. The variables RSex and RAge measure the respondents gender and age respectively. While we not necessarily expect causal relationships between gender, age and over-estimating immigration, these variables tend to correlate. Furthermore, we expect them to correlate with party identification and income. Therefore, we use them as control variables.
library(texreg)
# the regrssion model
m1 <- glm(over.estimate ~ HHInc + RSex + RAge,
family = binomial(link = "logit"),
data = data2)
# the regression table
screenreg(m1)
===========================
Model 1
---------------------------
(Intercept) 1.18 **
(0.39)
HHInc -0.11 ***
(0.02)
RSex 0.60 ***
(0.14)
RAge -0.00
(0.00)
---------------------------
AIC 1175.88
BIC 1195.71
Log Likelihood -583.94
Deviance 1167.88
Num. obs. 1049
===========================
*** p < 0.001; ** p < 0.01; * p < 0.05# from log-odds ratios to odds-ratios for HHInc (income)
exp(-0.11)[1] 0.8958341# reduction in odds-rations in % for every 1-unit increase in HHInc
(exp(-0.11) - 1) *100[1] -10.41659We do not find evidence for a relationship between party identification and over-estimating immigration. We do find evidence that more affluent respondents are less likely to over-estimate immigration. Increasing the income band of the respondent by 1, decrases the odds that the respondent will over-estimate immigration by 10 percent (the odds are multiplied by 0.896).
9.2.0.3 Exercise 3
What is the naive guess of over.estimate?
mean(data2$over.estimate)[1] 0.7235462The mean of over.estimate is 0.72. That means more people over-estimate immigration than not. Thus, the naive guess is 1 which means that people over-estimate immigration.
9.2.0.4 Exercise 4
What is the percentage of correctly predicted cases using the naive guess?
If we predict the naive guess for every observation in the dataset, we correctly classify 72 percent of all observations. We know that this is the case because the mean (the proportion of 1s) of over.estimate is 0.72.
9.2.0.5 Exercise 5
What is the percent of correctly predicted cases of your model and how does it compare to the naive guess?
# fitted values (1 fitted value for each respondent)
yhats <- predict(m1)
# converting the fitted values (which are log-odds ratios) to probabilities
# by applying the logit link function
pp <- exp(yhats) / (1 + exp(yhats))
# converting predicted probabilities to expected values,
# i.e., classifying outcomes into 0s and 1s
# if the predicted probability is > 0.5, we calssify as 1 and 0 otherwise
eval <- ifelse( pp > 0.5, yes = 1, no = 0)
# confusion matrix - cross-table of true outcomes against our
# predictions
cm <- table( truth = data2$over.estimate, prediction = eval )
# correct negatives and correct positives are on the diagonal
# false negatives and false positives are on the off-diagonal
# the percentage of correctly classified cases is the sum
# of correct predictions over the total number of predictions
# correct predictions (sum over diagonal elements in the confusion matrix)
good <- sum( diag( cm ) )
good[1] 763# total predictions (sum over all elements in the confusion matrix)
total <- sum( cm )
total[1] 1049# proportion correctly classified
good / total[1] 0.7273594# and percentage correctly classified
(good / total)*100[1] 72.73594The naive guess correctly classifies 72.3 percent of the cases. Our model does slightly better. It correctly classifies 72.7 percent of all cases. The improvement is small but the model is a contribution because it improves compared to not having a model at all.
9.2.0.6 Exercise 6
Add predictors to your model and justify the choice.
We include UKIP self-identification measured by the variable Ukip. Political parties take positions on immigration. UKIP is known to have a particularly restrictive stance. We might therefore expect the party’s adherents to overstate immigration levels
m2 <- glm(over.estimate ~ HHInc + RSex + RAge + as.factor(Ukip),
family = binomial(link = "logit"),
data = data2)
summary(m2)
Call:
glm(formula = over.estimate ~ HHInc + RSex + RAge + as.factor(Ukip),
family = binomial(link = "logit"), data = data2)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1548 -1.1477 0.6649 0.8447 1.2161
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.1744482 0.3928151 2.990 0.00279 **
HHInc -0.1064091 0.0163208 -6.520 7.04e-11 ***
RSex 0.5973469 0.1436707 4.158 3.21e-05 ***
RAge -0.0008077 0.0043483 -0.186 0.85263
as.factor(Ukip)1 0.0422746 0.4272243 0.099 0.92118
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1236.9 on 1048 degrees of freedom
Residual deviance: 1167.9 on 1044 degrees of freedom
AIC: 1177.9
Number of Fisher Scoring iterations: 49.2.0.7 Exercise 7
Are the added predictors jointly significant?
We carry out a joint hypothesis test to assess whether the added predictors are jointly significant. The appropriate test is the likelihood ratio test. It lets us compare nested models. Recall that nested means that the bigger model contains all variables that are also in the smaller model and some additional variables.
The null hypothesis is that both models predict the outcome equally well (the likelihoods are the same). That would mean that the added variables are insignificant. If the p value of the test is less than 0.05, we reject the null hypothesis. That would mean that the added variables are jointly significant.
We need the lmtest library which contains the likelihood ratio test function lrtest().
library(lmtest)
lrtest(m1, m2)Likelihood ratio test
Model 1: over.estimate ~ HHInc + RSex + RAge
Model 2: over.estimate ~ HHInc + RSex + RAge + as.factor(Ukip)
#Df LogLik Df Chisq Pr(>Chisq)
1 4 -583.94
2 5 -583.94 1 0.0098 0.921We fail to reject the null hypothesis and conclude that UKIP self-identification does not help to predict over-estimation.
9.2.0.8 Exercise 8
What is the new rate of correctly predicted cases? Is it better than the first model and how does it compare to the naive guess?
# this time we use the type="response" argument in the predict() function to directly
# estimate predicted probabilities (i.e., we can skip the step of converting fitted
# values to precited probabilities)
pp2 <- predict( m2, type = "response" )
# converting probabilites to expected values (for > 0.5, we assign a 1 and a 0 otherwise)
eval2 <- ifelse(pp2 > 0.5, yes = 1, no = 0)
# we construct the confusion matrix
cm2 <- table( truth = data2$over.estimate, prediction = eval2 )
# we calucate the percent of correct predictions
(sum(diag(cm2)) / sum(cm2))*100[1] 72.73594The model without UKIP self-identification correctly classified 72.7 percent of all observations in our sample. The model with UKIP identification does not increase this. Note, that we can never decrease the percent of correct classification by including variables. The predictive power of the model with either stay the same or increase. We say, it weakly increases (that means it either stays the same or increases). A good predictor increases predictive power substantially. How much is enough depends on the context and whether we care about predictive power. In a theory test - suppose we want to test whether income is causally related to over-estimating - we do not care by how much we increase predictive power of a model when including variables. In such a model the only purpose of party identification would be to guard against omitted variable bias.
9.2.0.9 Exercise 9
Vary the threshold for generating expected values and compute the percent correctly predicted cases again. How does it change?
The purpose of varying the classification threshold would be to reduce the number of false negatives or the number of false positives. We will always decrease overall prediction accuracy by varying the threshold. Thus changing the threshold is only justified if false positives are somehow more/less costly than false negatives.
We cannot think of a reason why it would be worse to misclassify a respondent as someone who over-estimates immigration than someone who does not over-estimate immigration. There are examples where this could be different (think of onsets of war or cancer detection tests).
Let’s inspect our confusion matrix.
cm2 prediction
truth 0 1
0 33 257
1 29 730We incorrectly classify 29 respondents as people who do not over-estimate immigration when in reality they do over-estimate. We also incorrectly classify 257 respondents as respondents who do over-estimate immigration when in reality they did not. Let’s reduce the latter. We can achieve this by increasing the threshold above 0.5. A higher threshold means that fewer people will be classified as over-estimators. We increase the threshold to 0.7.
# classification based on a threshold of 0.7
eval3 <- ifelse(pp2 > 0.7, yes = 1, no = 0)
# new confunsion matrix based on our 0.7 threshold
cm3 <- table( truth = data2$over.estimate, prediction = eval3 )
cm3 prediction
truth 0 1
0 168 122
1 264 495Clearly, we decreased the number of false (incorrect) positives (from 256 to 122). However, by doing so we increased the number of false (incorrect) negatives (from 28 to 264).
# new percent of correctly classified cases
(sum( diag(cm3) ) / sum(cm3)) * 100[1] 63.20305Our new classification rule, makes correct predictions for only 65 percent of all observations in the sample which is less the naive guess (72 percent).
9.2.0.10 Exercise 10
Vary a continuous predictor in a model and plot predicted probabilities over its range and include uncertainty estimates in the plot.
We illustrate the effect of income by varying it from minimum to maximum. We have to pick values for the control variables UKIP identification, age, and gender. Age is continuous, so we can pick the mean. Gender and UKIP identification are categorical, so we pick the modes.
# find the mode of party identification
table(data2$Ukip)
0 1
1018 31 # find the mode of gender
table(data2$RSex)
1 2
478 571 The mode of UKIP identification is 0 which corresponds to not identifying with UKIP. The mode of gender is 2 which corresponds to female. The mean of age in our sample is 50. Let’s save these values in objects.
ukip.mode <- 0
gender.mode <- 2
age.mean <- 50Next, we find the minimum and maximum of income and then create a variable that varies income from minimum to maximum in 100 steps.
# find the minimum and maximum of income
range(data2$HHInc)[1] 1 17# vary income from minimum to maximum in 100 steps
income.sequence <- seq(from = 1, to = 17, length.out = 100)Now, we can predict the probabilities that respondents with varying income who do not affiliate with any of the big parties in the UK, who are 50 years old and female will over-estimate immigration. We have to set the argument type="response" to obtain predicted probabilities. We also have to set the argument se.fit=TRUE which will return a standard error for every predicted probability. Finally, we have to set all variables (covariates) to the values that we specified above.
# 100 predicted probabilities of over-estimating (1 for each income step)
pp3 <- predict(m2, type = "response", se.fit = TRUE,
newdata = data.frame(HHInc = income.sequence,
RSex = gender.mode,
RAge = age.mean,
Ukip = ukip.mode))This has created a list of our output, but we would like it to be in a clean dataframe. We can extract the different parts, using the standard errors to estimate the confidence intervals in the process.
prediction <- pp3$fit
ses <- pp3$se.fit
upr <- prediction + 1.96*ses
lwr <- prediction - 1.96*ses
income_predict <- data.frame(income.sequence, prediction, upr, lwr)Now, we can create a plot with predicted probabilities and confidence intervals.
gg_income_pred <- ggplot(data = income_predict, # dataset to work from
mapping = aes(x = income.sequence, # x axis
y = prediction)) + # y axis
geom_pointrange(mapping = aes(ymax = upr, # points with confidence intervals
ymin = lwr)) +
geom_ribbon(mapping = aes(ymax = upr, # shaded area of confidence intervals
ymin = lwr),
alpha = 0.5) + # make semi-transparent
labs(x = "Household income",
y = "Predicted probability of over-estimation")
gg_income_pred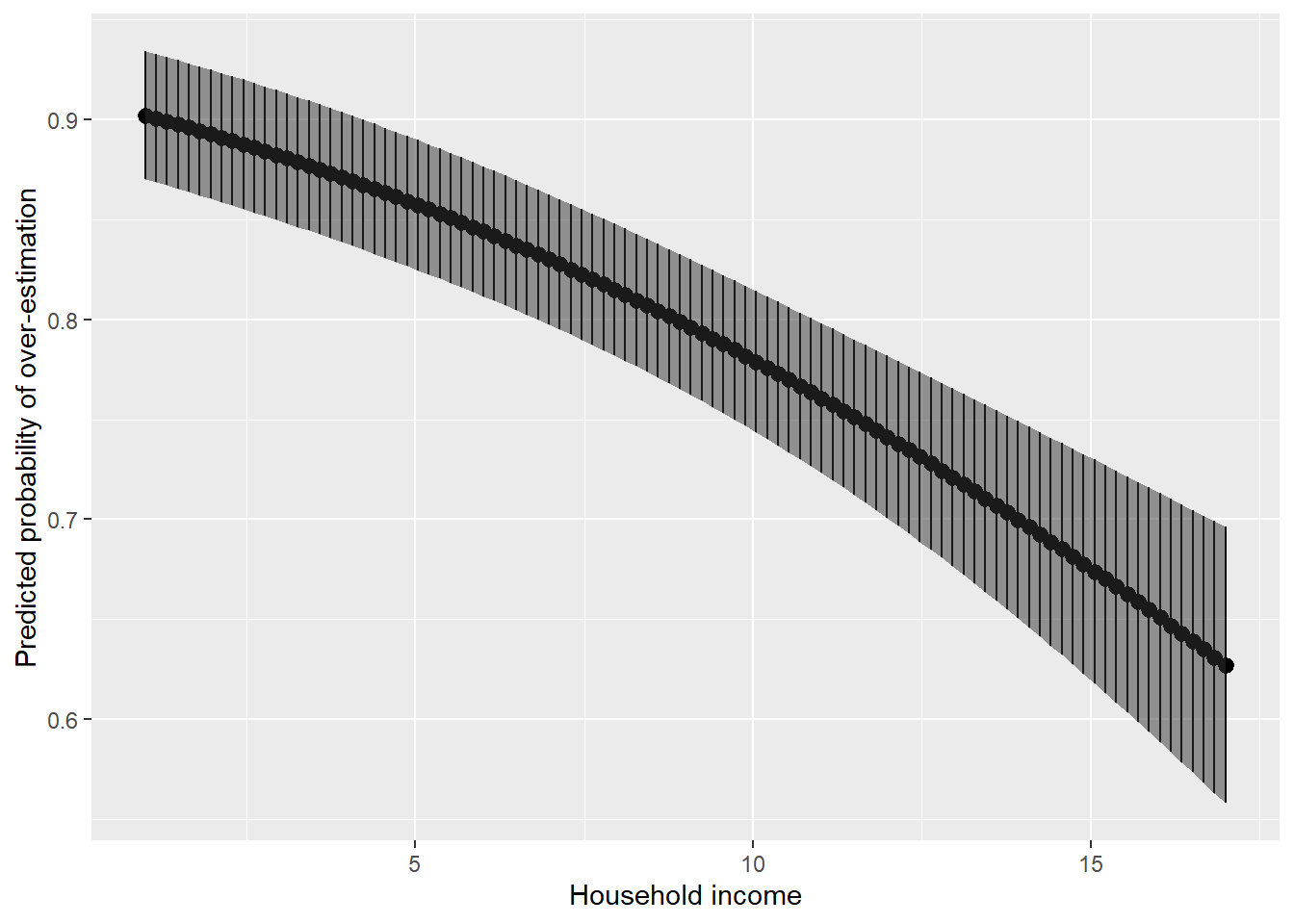
Given our set of covariate values (50-year-old women who do not affiliate with UKIP), the effect of income is no trivial. The predicted probability of over-estimating the level of immigration decreases from just over 90 percent to around 65 percent.