Chapter 6 Multiple linear regression models (II)

6.1 Seminar – in class exercises

In the first part of this seminar, we cover R^2 and adjusted R^2. In the second, we cover interactions. First, an interaction between continuous and binary independent variable and second, between two continuous variables. We also show the F test.

To start with, load the foreign library and the texreg library.

library(foreign) # to load non-native file formats
library(texreg) # to create better looking regression tables
library(marginaleffects) # marginal effects plotting

Warning: package 'marginaleffects' was built under R version 4.2.3

In case library(texreg) throws an error message, you have to install the package first. A package is like an app on your mobile. It adds additional functionality. You need to install it only once. To install the package run install.packages("texreg"). Then load the library library(texreg). Do the same for install.packages("marginaleffects").

6.1.1 Loading Data

We will use the small version of the Quality of Government data from 2012 again (QoG2012.csv), focusing on four variables:

Variable	Description
`former_col`	0 = not a former colony 1 = former colony
`undp_hdi`	UNDP Human Development Index. Higher values mean better quality of life
`wbgi_cce`	Control of corruption. Higher values mean better control of corruption
`wdi_gdpc`	GDP per capita in US dollars

qog <- read.csv("https://raw.githubusercontent.com/QMUL-SPIR/Public_files/master/datasets/QoG2012.csv")

qog <- select(qog, # subset qog to four variables
              former_col,
              undp_hdi,
              wbgi_cce,
              wdi_gdpc)

summary(qog)

   former_col        undp_hdi         wbgi_cce           wdi_gdpc      
 Min.   :0.0000   Min.   :0.2730   Min.   :-1.69953   Min.   :  226.2  
 1st Qu.:0.0000   1st Qu.:0.5390   1st Qu.:-0.81965   1st Qu.: 1768.0  
 Median :1.0000   Median :0.7510   Median :-0.30476   Median : 5326.1  
 Mean   :0.6289   Mean   :0.6982   Mean   :-0.05072   Mean   :10184.1  
 3rd Qu.:1.0000   3rd Qu.:0.8335   3rd Qu.: 0.50649   3rd Qu.:12976.5  
 Max.   :1.0000   Max.   :0.9560   Max.   : 2.44565   Max.   :63686.7  
                  NA's   :19       NA's   :2          NA's   :16

Let’s create a copy of the dataset and then remove all missing values.

# copy of original dataset
qog_full <- qog

To remove all missing values at once, we use drop_na() on the whole dataset. We also show you here a way to do this using base R’s apply() function. If you are interested in learning more about how apply() functions work, check the help page (run ?apply).

# drop all missing values
qog <- qog[apply(qog, 1, function(x) all(!is.na(x)) ), ]

# simpler way
qog <- drop_na(qog_full)

6.1.2 R Squared

Let’s say we want to predict the quality of life. Our variable that approximates this is called undp_hdi (the United Nations human development index). The variable is continuous and has a theoretical range from 0 to 1. Larger values correspond to better life quality.

If we did not have any information on a country, our best prediction for every country would be the mean of undp_hdi. We would make some mistakes. But on average, this would be our best prediction. Let’s confirm that this is the case.

# mean of undp_hdi
y_bar <- mean(qog$undp_hdi)

round(y_bar, digits = 2)

[1] 0.7

Our mean is 0.7. If we predict the mean for every country, we will make some mistakes. These mistakes are the differences between the actual values of undp_hdi in every country and the mean of undp_hdi.

# deviations from the mean
deviations <- (qog$undp_hdi - y_bar)

It’s always going to be true that the sum of the average deviations is 0. This is a property of the mean.

# sum of deviations from ybar is always zero (with rounding, extremely close to 0)
sum(deviations)

[1] 4.163336e-15

We will now square the deviations from the mean.

# squared deviations from the mean
sq_deviations <- deviations^2

The squared deviations from the mean capture the overall variability of our variable undp_hdi. At this point you might notice that what we did so far is the first step to getting variance. Dividing the sum of the squared deviations by $n-1$ would give us the variance of undp_hdi. The variance quantifies the variability of a variable.

Let’s do this:

total_variance <- sum(sq_deviations) / (length(qog$undp_hdi) - 1)
total_variance

[1] 0.03277426

The overall variance of undp_hdi is 0.0327743.

Let’s say, we have additional information about a country like for example its wealth. Wealth is measured by the variable wdi_gdpc. We now run a linear model where we predict undp_hdi using the information in wdi_gdpc. If the regression coefficient of wdi_gdpc is significant, that means that the variables are associated. This in turn means that we can explain some of the variability in undp_hdi using variability in wdi_gdpc.

# we regress undp_hdi on wdi_gdpc
m1 <- lm( undp_hdi ~ wdi_gdpc, data = qog)
screenreg(m1)


=======================
             Model 1   
-----------------------
(Intercept)    0.59 ***
              (0.01)   
wdi_gdpc       0.00 ***
              (0.00)   
-----------------------
R^2            0.49    
Adj. R^2       0.49    
Num. obs.    172       
=======================
*** p < 0.001; ** p < 0.01; * p < 0.05

The coefficient of wdi_gdpc is indeed significant. Let’s plot the relationship in a scatterplot and draw the regression line.

# the scatterplot
gg_hdi_wealth <- ggplot(data = qog,
                        mapping = aes(x = wdi_gdpc,
                                      y = undp_hdi)) +
  geom_point() +
  labs(x = "GDP per captia in US dollars",
       y = "Human Development Index") +
  geom_smooth(method = "lm") # regression line

gg_hdi_wealth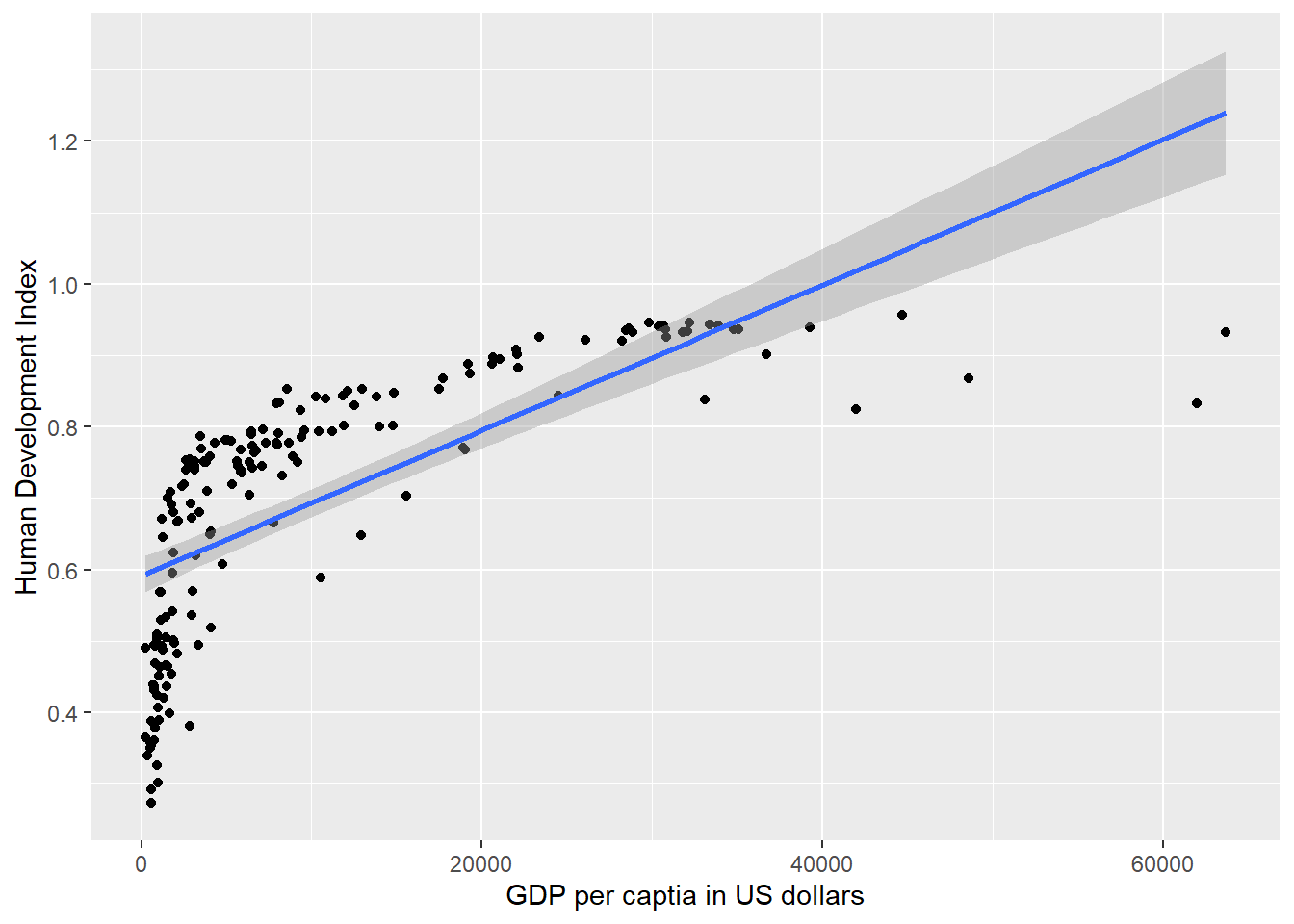

This model looks awful. We over-predict quality of live for poor countries. We under-predict for medium wealth levels and over-predict for rich countries. We will return to this problem later.

For now, you should see that using the variability in wdi_gdpc we actually explain some of the variability in undp_hdi. We do not explain all of the variability. There are still differences between our predictions (the points on the line) and actual outcomes. Were we to explain all of the variability, all of the points would be on the line. They are not. They never will be in real-life applications. The social world is complex. However, we can ask: “How much of the variability in undp_hdi do we explain using the variability in wdi_gdpc.

To answer this question, we first extract a fitted value for every observation in the dataset. Recall that a fitted value is a point on the line. Hence, we take the regression equation $\hat{Y} = 0.5855759 + 0.000102 \times \textrm{GDP per capita}$ and plug in the value of wdi_gdpc for every row in the dataset.

Actually, R has already done that for us. We can access the fitted values from our model object m1 like so.

fitted_vals <- m1$fitted.values

Now, we take the same steps as we did earlier. We take the deviations between the actual outcome of undp_hdi and our model predictions (the fitted values). These differences are the mistakes, we make they are called residuals.

# residuals
resids <- (qog$undp_hdi - fitted_vals)

Actually, R did that for us as well. We could have accessed the residuals as m1$residuals. We again square the deviations between the model predictions and the actual outcomes.

# squared residuals
sq_resids <- resids^2

The squared residuals are the variability in undp_hdi which we have NOT explained with the variability in wdi_gdpc.

R^2 is then: 1 - unexplained variability / total variability. R^2, therefore, answers the question “how much of the total variability in undp_hdi do we explain using variability in wdi_gdpc?”

R.sq <- 1 - sum(sq_resids) / sum(sq_deviations)
R.sq

[1] 0.4888135

We have successfully estimated R^2. There are other ways to get there. For instance, we could compare the variances instead of sums of squared deviations.

Note: The difference between our estimate of R^2 and the one from the regression table is due to rounding error. We get the same value if we use the round() function to round to 2 digits like so:

round(R.sq, digits = 2)

[1] 0.49

6.1.2.1 R Squared - Approach 2

Let’s take the unexplained variance of undp_hdi instead of the unexplained sum of squares.

# unexplained variance
unexplained_variance <- sum(sq_resids) / (length(sq_resids) - 1)

R^2 is then 1 - unexplained variance over total variance.

R.sq <- 1 - unexplained_variance / total_variance
R.sq

[1] 0.4888135

6.1.2.2 R Squared - Approach 3

Let’s use the explained sum of squares instead of the unexplained sum of squares, i.e., \[R^2 = \frac{ESS}{TSS}\].

# explained sum of squares
ESS <- sum((fitted_vals - y_bar)^2)

# R^2
R.sq <- ESS/ sum(sq_deviations)
R.sq

[1] 0.4888135

6.1.2.3 R Squared - Approach 4

You may have already noticed that R^2 looks very similar to the correlation coefficient. That’s right. In fact, we can quickly estimate R^2 by taking the squared correlation between our fitted values and the actual outcomes.

R.sq <- cor(m1$fitted.values, qog$undp_hdi)^2
R.sq

[1] 0.4888135

6.1.2.4 Adjusted R^2

R^2 always weakly increases if we include more X variables into our model. The reason is that the correlation between two variables is never exactly zero. That means in any sample, two variables are always related to some degree. They may not be related in the same way in the population, however. So, the relationship between two variables that we see in our sample may just be noise.

Yet, R^2 increases whenever two variables are correlated. R^2 never decreases. Adjusted R^2 accounts for the number of predictors that we have added two our model by adding a penalty that increases as we increase the number of X variables in our model. The penalty looks like this:

We multiply R^2 by $\frac{n-1}{n-k-1}$, where $n$ is the number of observations and $k$ is the number of X variables. So, assuming our sample size is 158 and we add 1 predictor to our model that so far only included political stability, we would multiply R^2 by

# number of observations
n <- length(sq_resids)
# number of X variables
k <- length(m1$coefficients) - 1
# penalty
penalty <- (n-1) / (n-k-1)
adj.R.sq <- 1 - penalty * (sum(sq_resids) / sum(sq_deviations))
adj.R.sq

[1] 0.4858065

Since the formula for adjusted R^2 is: \[ 1 - \frac{n-1}{n-k-1} \times \frac{\mathrm{Sum\;of\;unexplained\;variability}}{\mathrm{Sum\;of\;total\;variability}} \]

we can estimate adjusted R^2 by rearranging the formula to:

\[ 1 - (1-R^2) \times \frac{n-1}{n-k-1} \] Let’s compute adjusted R^2 directly from R^2:

adj.R.sq <- 1 - (1 - R.sq) * penalty
adj.R.sq

[1] 0.4858065

6.1.3 The Relationship between Institutional Quality and Quality of Life by Colonial Past

Let’s create a scatterplot between wbgi_cce and undp_hdi and color the points based on the value of former_col. If this code is very confusing to you, look at the section [Going further with ggplot2].

# scatterplot of institiution quality and quality of life, by colonial status
gg_wbgi_hdi_col <- ggplot(data = qog, # dataset to work from
                          mapping = aes(
                            x = wbgi_cce, # x axis
                            y = undp_hdi, # y axis
                            colour = factor(former_col))) + # make sure former_col is treated as nominal
  geom_point() + # make it a scatterplot
  labs(title = "Relation between institutional quality and HDI by colonial past", # set title
       x = "Quality of institutions", # x axis title
       y = "Human Development Index") + # y axis title
  scale_colour_discrete( # change legend
    name = "Colonial past", # legend title
    labels = c("Never colonised", # legend labels
               "Former colony")
  )

gg_wbgi_hdi_col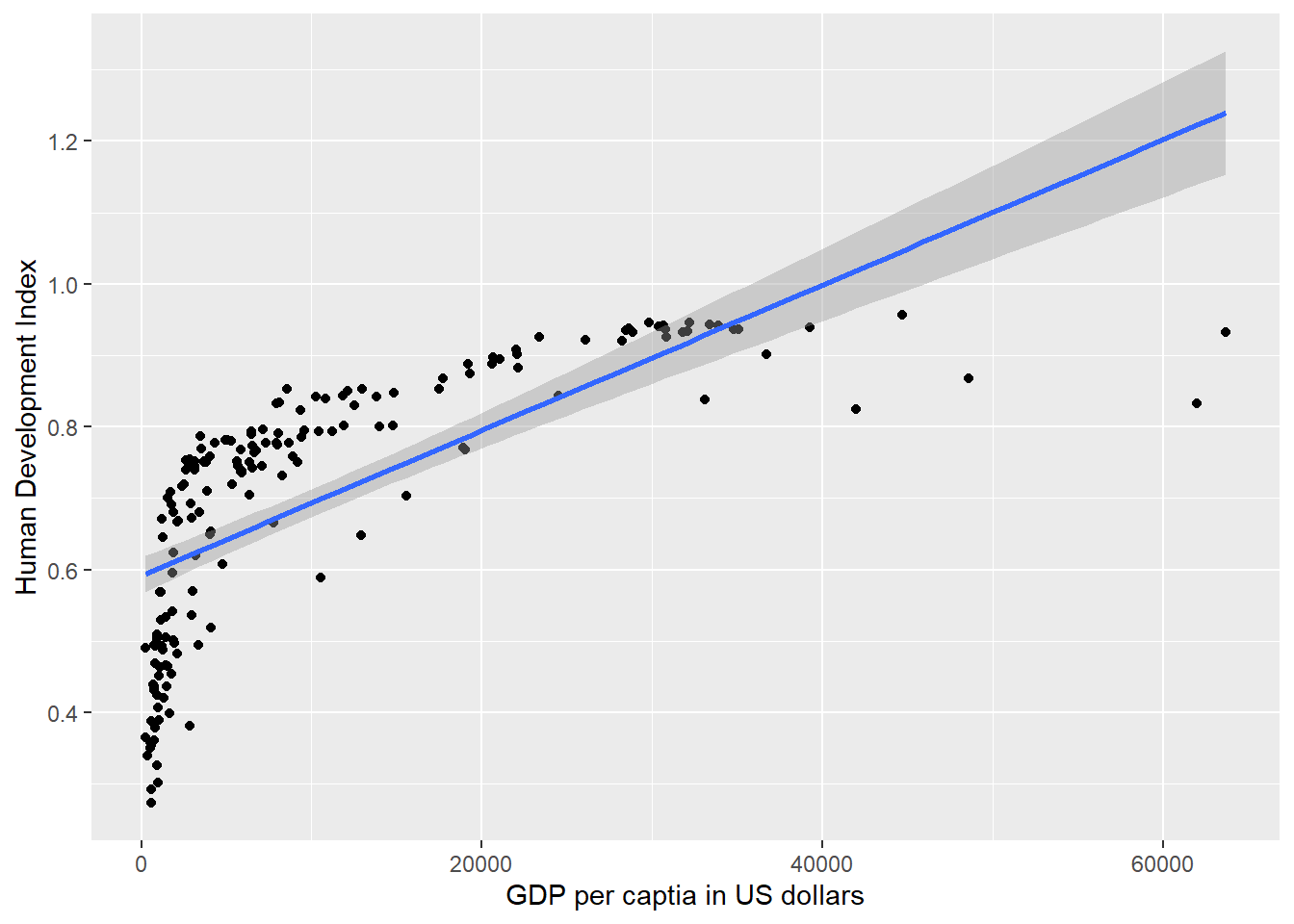

To explain the level of development with quality of institutions is intuitive. We could add the colonial past dummy, to control for potential confounders. Including a dummy gives us the difference between former colonies and not former colonies. It therefore shifts the regression line parallelly. We have looked at binary variables in the last weeks. To see the effect of a dummy again, refer to the extra info at the bottom of page.

6.1.4 Interactions: Continuous and Binary

From the plot above, we can tell that the slope of the line (the effect of institutional quality) is probably different in countries that were colonies and those that were not. We say: the effect of institutional quality is conditional on colonial past.

To specify an interaction term, we use the asterisk (*)

	Example
`*`	`AB` - In addition to the interaction term (AB), both the constituents (A and B) are automatically included.

m2 <- lm(undp_hdi ~ wbgi_cce * former_col, data = qog)
screenreg( m2 )


===============================
                     Model 1   
-------------------------------
(Intercept)            0.79 ***
                      (0.02)   
wbgi_cce               0.08 ***
                      (0.01)   
former_col            -0.12 ***
                      (0.02)   
wbgi_cce:former_col    0.05 ** 
                      (0.02)   
-------------------------------
R^2                    0.56    
Adj. R^2               0.55    
Num. obs.            172       
===============================
*** p < 0.001; ** p < 0.01; * p < 0.05

We set our covariate former_col to countries that weren’t colonized and then second, to ex colonies. We vary the quality of institutions from -1.7 to 2.5 which is roughly the minimum to the maximum of the variable.

NOTE: We know the range of values for wbgi_cce from the summary statistics we obtained after loading the dataset at the beginning of the seminar. You can also use the range() function.

# minimum and maximum of the quality of institutions
range(qog$wbgi_cce)

[1] -1.699529  2.445654

We now illustrate what the interaction effect does. To anticipate, the effect of the quality of institutions is now conditional on colonial past. That means, the two regression lines will have different slopes.

We make use of the predict() function to draw both regression lines into our plot. First, we need to vary the institutional quality variable from its minimum to its maximum. We use the seq() (sequence) function to create 10 different institutional quality values. Second, we create two separate covariate datasets. In the first, x1, we set the former_col variable to never colonies. In the second, x2, we set the same variable to ex colonies. We then predict the fitted values y_hat1, not colonised countries, and y_hat2, ex colonies.

# sequence of 10 institutional quality values
institutions_seq <- seq(from = -1.7, to = 2.5, length.out = 10)

# covariates for not colonies
x1 <- data.frame(former_col = 0, wbgi_cce = institutions_seq)
# look at our covariates
head(x1)

  former_col   wbgi_cce
1          0 -1.7000000
2          0 -1.2333333
3          0 -0.7666667
4          0 -0.3000000
5          0  0.1666667
6          0  0.6333333

# covariates for colonies
x2 <- data.frame(former_col = 1, wbgi_cce = institutions_seq)
# look at our covariates
head(x2)

  former_col   wbgi_cce
1          1 -1.7000000
2          1 -1.2333333
3          1 -0.7666667
4          1 -0.3000000
5          1  0.1666667
6          1  0.6333333

# predict fitted values for countries that weren't colonised 
yhat1 <- predict(m2, newdata = x1)

# add to data
x1$prediction <- yhat1

# predict fitted values for countries that were colonised
yhat2 <- predict(m2, newdata = x2)

# add to data
x2$prediction <- yhat2

We now have the predicted outcomes for varying institutional quality. Once for the countries that were former colonies and once for the countries that were not.

We will re-draw our earlier plot. In addition, right below the plot() function, we use the lines() function to add the two regression lines. The function needs to arguments x and y which represent the coordinates on the respective axes. On the x axis we vary our independent variable quality of institutions. On the y axis, we vary the predicted outcomes.

We add two more arguments to our lines() function. The line width is controlled with lwd and we set the colour is controlled with col which we set to the first and second colours in the colour palette respectively.

# main plot
interaction_plot <- gg_wbgi_hdi_col +
  geom_line(data = x1, # add lines for each prediction
            mapping = aes(x = institutions_seq,
                          y = yhat1)) +
  geom_line(data = x2,
            mapping = aes(x = institutions_seq,
                          y = yhat2)) 

interaction_plot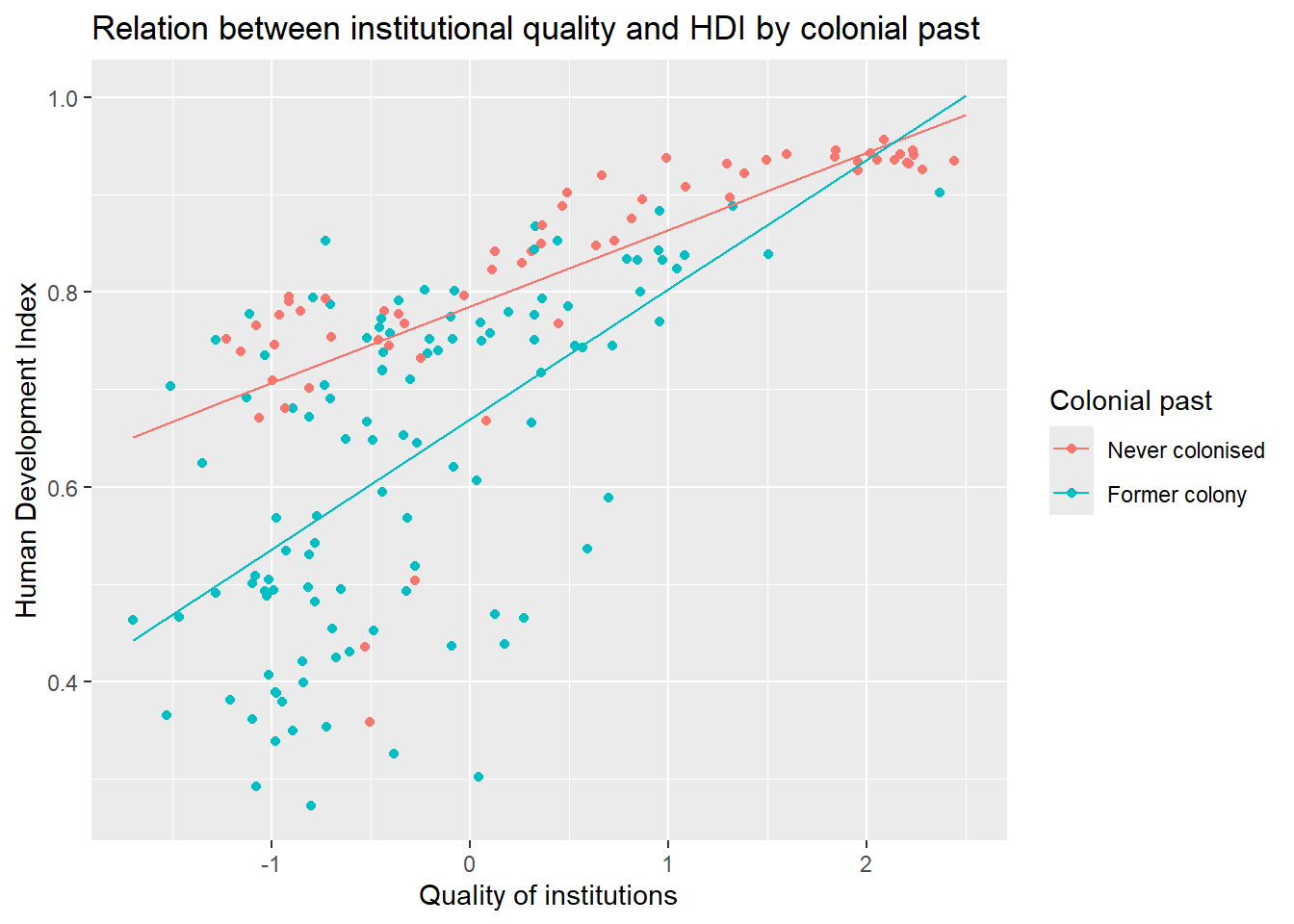

As you can see, the line is steeper for ex colonies than for countries that were never colonised. That means the effect of institutional quality on human development is conditional on colonial past. Institutional quality matters more in ex colonies.

Let’s examine the effect sizes of institutional quality conditional on colonial past.

\[\begin{align} \hat{y} & = & \beta_{0} + \beta_{1} \times \mathrm{wbgi_cce} + \beta_{2} \times \mathrm{former\_col} + \beta_{3} \times \mathrm{wbgi_cce} \times \mathrm{former\_col} \\ \hat{y} & = & 0.79 + 0.08 \times \mathrm{wbgi_cce} + -0.12 \times \mathrm{former\_col} + 0.05 \times \mathrm{wbgi_cce} \times \mathrm{former\_col} \end{align}\]

There are now two scenarios. First, we look at never coloines or second, we look at ex colonies. Let’s look at never colonies first.

If a country was never a colony, all terms that are multiplied with former_col drop out.

\[\begin{align} \hat{y} & = & 0.79 + 0.08 \times \mathrm{wbgi_cce} + -0.12 \times 0 + 0.05 \times 0 \\ \hat{y} & = & 0.79 + 0.08 \times \mathrm{wbgi_cce} \end{align}\]

Therefore, the effect of the quality of institutions (measured by wbgi_cce) in never colonies is just the coefficient of wbgi_cce $\beta_1 = 0.08$.

In the second scenario, we are looking at ex colonies. In this case none of the terms drop out. From our original equation:

\[\begin{align} \hat{y} & = & 0.79 + 0.08 \times \mathrm{wbgi_cce} + -0.12 \times \mathrm{former\_col} + 0.05 \times \mathrm{wbgi_cce} \times \mathrm{former\_col} \\ \hat{y} & = & 0.79 + 0.08 \times \mathrm{wbgi_cce} + -0.12 \times 1 + 0.05 \times \mathrm{wbgi_cce} \times 1 \\ \hat{y} & = & 0.79 -0.12 + 0.08 \times \mathrm{wbgi_cce} + 0.05 \times \mathrm{wbgi_cce} \\ \hat{y} & = & 0.67 + 0.08 \times \mathrm{wbgi_cce} + 0.05 \times \mathrm{wbgi_cce} \end{align}\]

The effect of the quality of institutions is then: $\beta_1 + \beta_3 = 0.08 + 0.05 = 0.13$.

The numbers also tell us that the effect of the quality of institutions is bigger in ex colonies. For never colonies the effect is $0.08$ for every unit-increase in institutional quality. For ex colonies, the corresponding effect is $0.13$.

The table below summarises the interaction of a continuous variable with a binary variable in the context of our regression model.

Ex Colony	Intercept	Slope
0 = never colony	$\beta_0$ $= 0.79$	$\beta_1$ $= 0.08$
1 = ex colony	$\beta_0 + \beta_2$ = $0.79 + -0.12 = 0.67$	$\beta_1 + \beta_3$ $= 0.08 + 0.05 = 0.13$

6.1.5 Non-Linearities

We can use interactions to model non-linearities. Let’s suppose we want to illustrate the relationship between GDP per capita and the human development index.

We draw a scatter plot to investigate the relationship between the quality of life (hdi) and wealth (gdp/capita). We saw this plot earlier.

# the scatterplot
gg_hdi_wealth <- ggplot(data = qog,
                        mapping = aes(x = wdi_gdpc,
                                      y = undp_hdi)) +
  geom_point() +
  labs(x = "GDP per captia in US dollars",
       y = "Human Development Index") +
  geom_smooth(method = "lm",
              se = F) # regression line

gg_hdi_wealth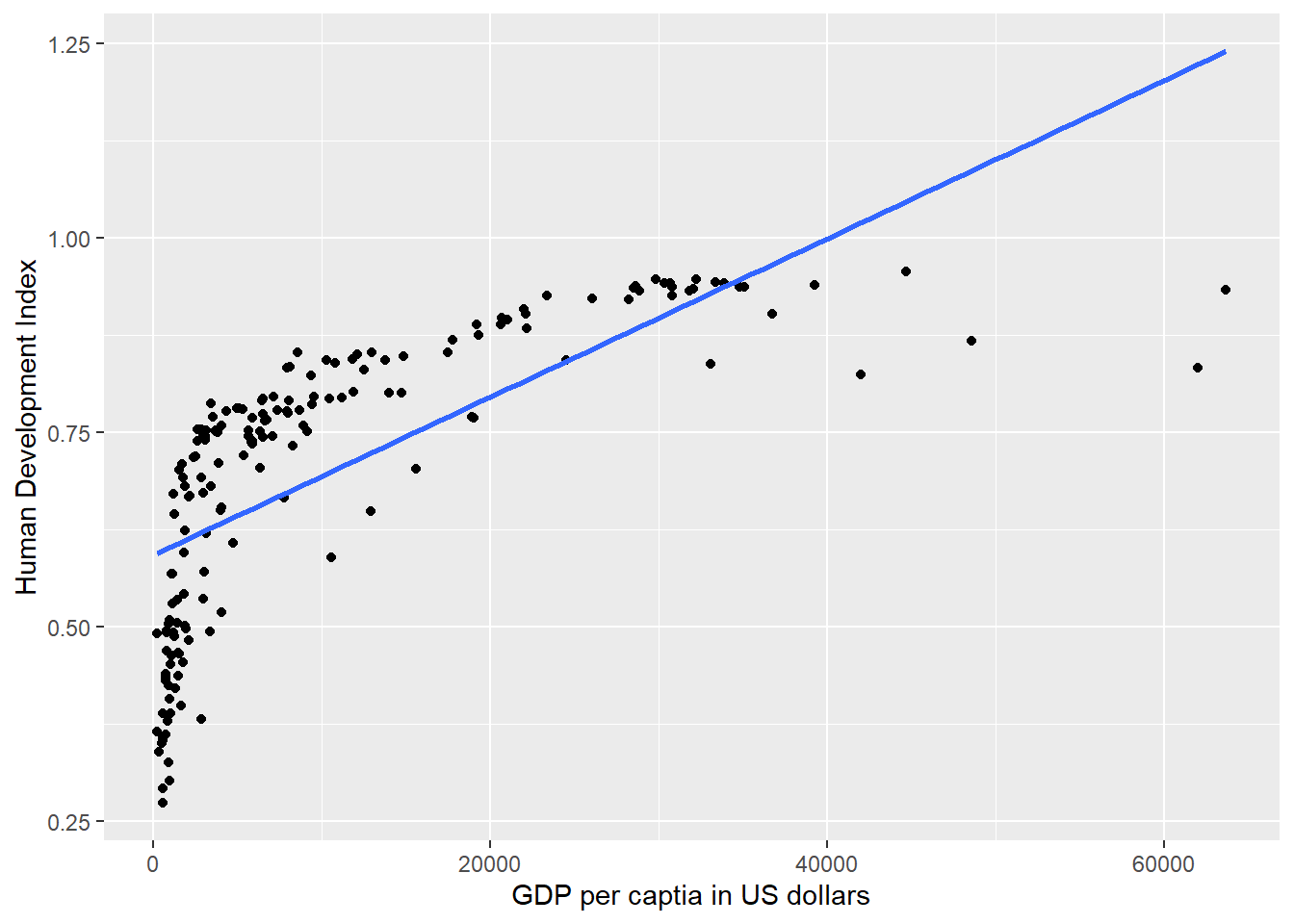

It’s easy to see, that the relationship between GDP per capita and the Human Development Index is not linear. Increases in wealth rapidly increase the quality of life in poor societies. The richer the country, the less pronounced the effect of additional wealth. We would mis-specify our model if we do not take the non-linear relationship into account.

Let’s go ahead and mis-specify our model!

# a mis-specified model
bad_model <- lm(undp_hdi ~ wdi_gdpc, data = qog)
screenreg(bad_model)


=======================
             Model 1   
-----------------------
(Intercept)    0.59 ***
              (0.01)   
wdi_gdpc       0.00 ***
              (0.00)   
-----------------------
R^2            0.49    
Adj. R^2       0.49    
Num. obs.    172       
=======================
*** p < 0.001; ** p < 0.01; * p < 0.05

We detect a significant linear relationship. The effect may look small because the coefficient rounded to two digits is zero. But remember, this is the effect of increasing GDP/capita by $1$ US dollar on the quality of life. That effect is naturally small but it is probably not small when we increase wealth by $1000$ US dollars.

However, our model would also entail that for every increase in GDP/capita, the quality of life increases on average by the same amount. We saw from our plot that this is not the case. The effect of GDP/capita on the quality of life is conditional on the level of GDP/capita. If that sounds like an interaction to you, then that is great because, we will model the non-linearity by raising the GDP/capita to a higher power. That is in effect an interaction of the variable with itself. GDP/capita raised to the second power, e.g. is GDP/capita * GDP/capita.

6.1.5.1 Polynomials

We know from school that polynomials like $x^2$, $x^3$ and so on are not linear. In fact, $x^2$ can make one bend, $x^3$ can make two bends and so on.

Our plot looks like the relationship is quadratic. So, we use the poly() function in our linear model to raise GDP/capita to the second power like so: poly(wdi_gdpc, 2).

better_model <- lm(undp_hdi ~ poly(wdi_gdpc, 2), data = qog)
screenreg(list(bad_model, better_model), 
           custom.model.names = c("Bad model", "Better model"))


============================================
                    Bad model   Better model
--------------------------------------------
(Intercept)           0.59 ***    0.70 ***  
                     (0.01)      (0.01)     
wdi_gdpc              0.00 ***              
                     (0.00)                 
poly(wdi_gdpc, 2)1                1.66 ***  
                                 (0.10)     
poly(wdi_gdpc, 2)2               -1.00 ***  
                                 (0.10)     
--------------------------------------------
R^2                   0.49        0.67      
Adj. R^2              0.49        0.66      
Num. obs.           172         172         
============================================
*** p < 0.001; ** p < 0.01; * p < 0.05

It is important to note, that in the better model the effect of GDP/capita is no longer easy to interpret. We cannot say for every increase in GDP/capita by one dollar, the quality of life increases on average by this much. No, the effect of GDP/capita depends on how rich a country was to begin with.

It looks like our model that includes the quadratic term has a much better fit. The adjusted R^2 increases by a lot. Furthermore, the quadratic term, poly(gdp_capita, 2)2 is significant. That indicates that newly added variable improves model fit. We can run an F-test with anova() function which will return the same result. The F-test would be useful when we add more than one new variable, e.g. we could have raised GDP_captia to the power of 5 which would have added four new variables.

# f test
anova(bad_model, better_model)

Analysis of Variance Table

Model 1: undp_hdi ~ wdi_gdpc
Model 2: undp_hdi ~ poly(wdi_gdpc, 2)
  Res.Df    RSS Df Sum of Sq     F    Pr(>F)    
1    170 2.8649                                 
2    169 1.8600  1    1.0049 91.31 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We can interpret the effect of wealth (GDP/capita) on the quality of life (human development index) by predicting the fitted values of the human development index given a certain level of GDP/capita. We will vary GDP/captia from its minimum in the data to its maximum and the plot the results which is a good way to illustrate a non-linear relationship.

Step 1: We find the minimum and maximum values of GDP/capita.

# find minimum and maximum of per capita gdp
range(qog$wdi_gdpc)

[1]   226.235 63686.676

Step 2: We predict fitted values for varying levels of GDP/captia (let’s create 100 predictions).

# our sequence of 100 GDP/capita values
gdp_seq <- seq(from = 226, to = 63686, length.out = 100)

# we set our covarite values (here we only have one covariate: GDP/captia)
x <- data.frame(wdi_gdpc = gdp_seq)

# we predict the outcome (human development index) for each of the 100 GDP levels
y_hat <- predict(better_model, newdata = x)

# add to data
x$prediction <- y_hat

Step 3: Now that we have created our predictions. We plot again and then we add the bad.model using abline and we add our non-linear version better.model using the lines() function.

gg_hdi_wealth <- gg_hdi_wealth +
  geom_line(data = x,
            mapping = aes(x = gdp_seq,
                          y = prediction),
            colour = "red")

gg_hdi_wealth

`geom_smooth()` using formula = 'y ~ x'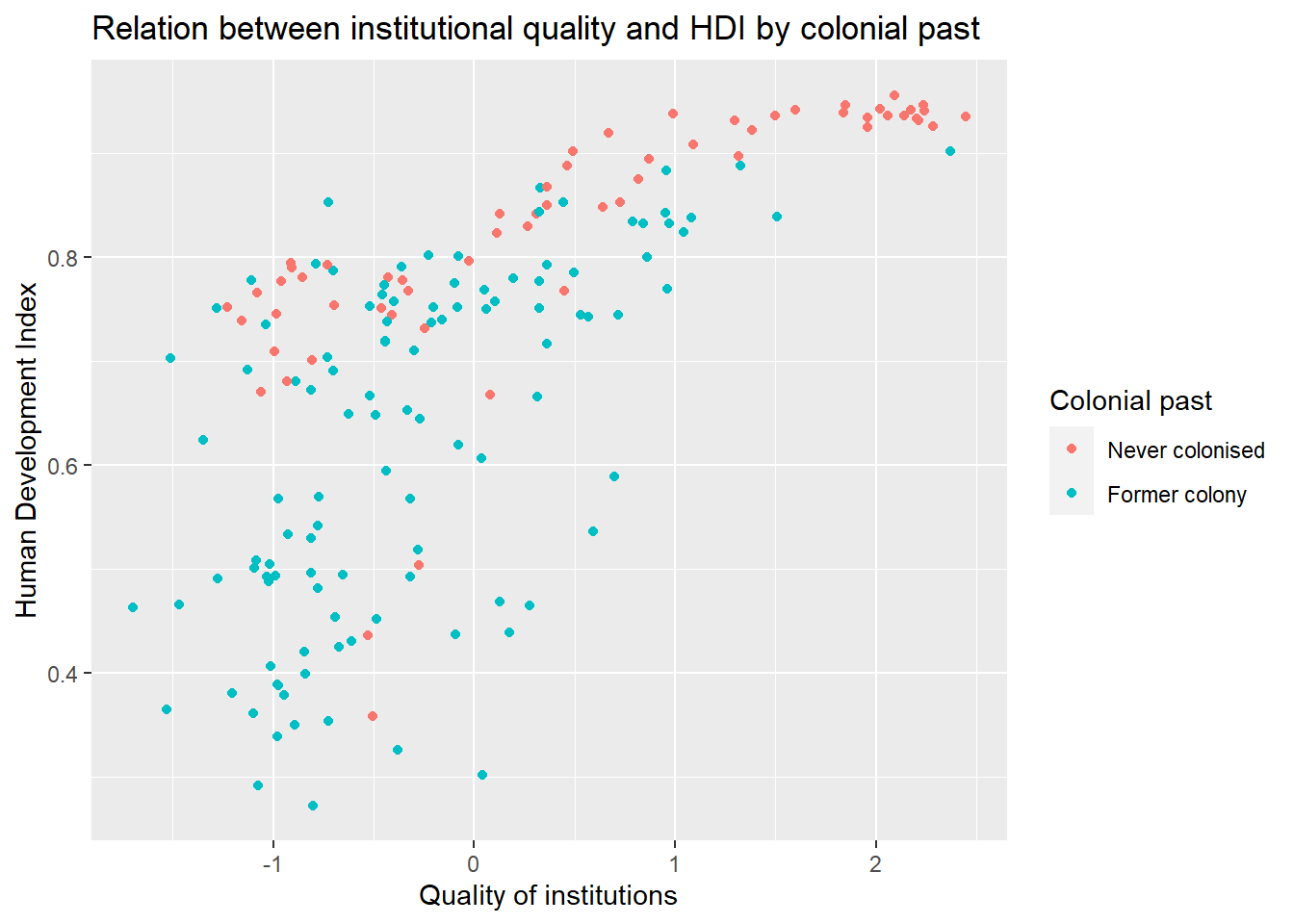

We could estimate even_better_model with GDP/capita raised to the power of three to determine whether the data fit improves. We can show this visually and with an F test.

# estimate even better model with gdp/capita^3
even_better_model <- lm(undp_hdi ~ poly(wdi_gdpc, 3), data = qog)

# f test
anova(better_model, even_better_model)

Analysis of Variance Table

Model 1: undp_hdi ~ poly(wdi_gdpc, 2)
Model 2: undp_hdi ~ poly(wdi_gdpc, 3)
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1    169 1.8600                                  
2    168 1.4414  1   0.41852 48.779 6.378e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The F test demonstrates that this new model is statistically significantly even better.

# predict the outcome (human development index) for each of the 100 GDP levels
y_hat2 <- predict(even_better_model, newdata = x)

# add prediction to data
x$cube_prediction <- y_hat2

# add prediction to plot
gg_hdi_wealth <- gg_hdi_wealth +
  geom_line(data = x,
            mapping = aes(x = gdp_seq,
                          y = cube_prediction),
            colour = "green")

gg_hdi_wealth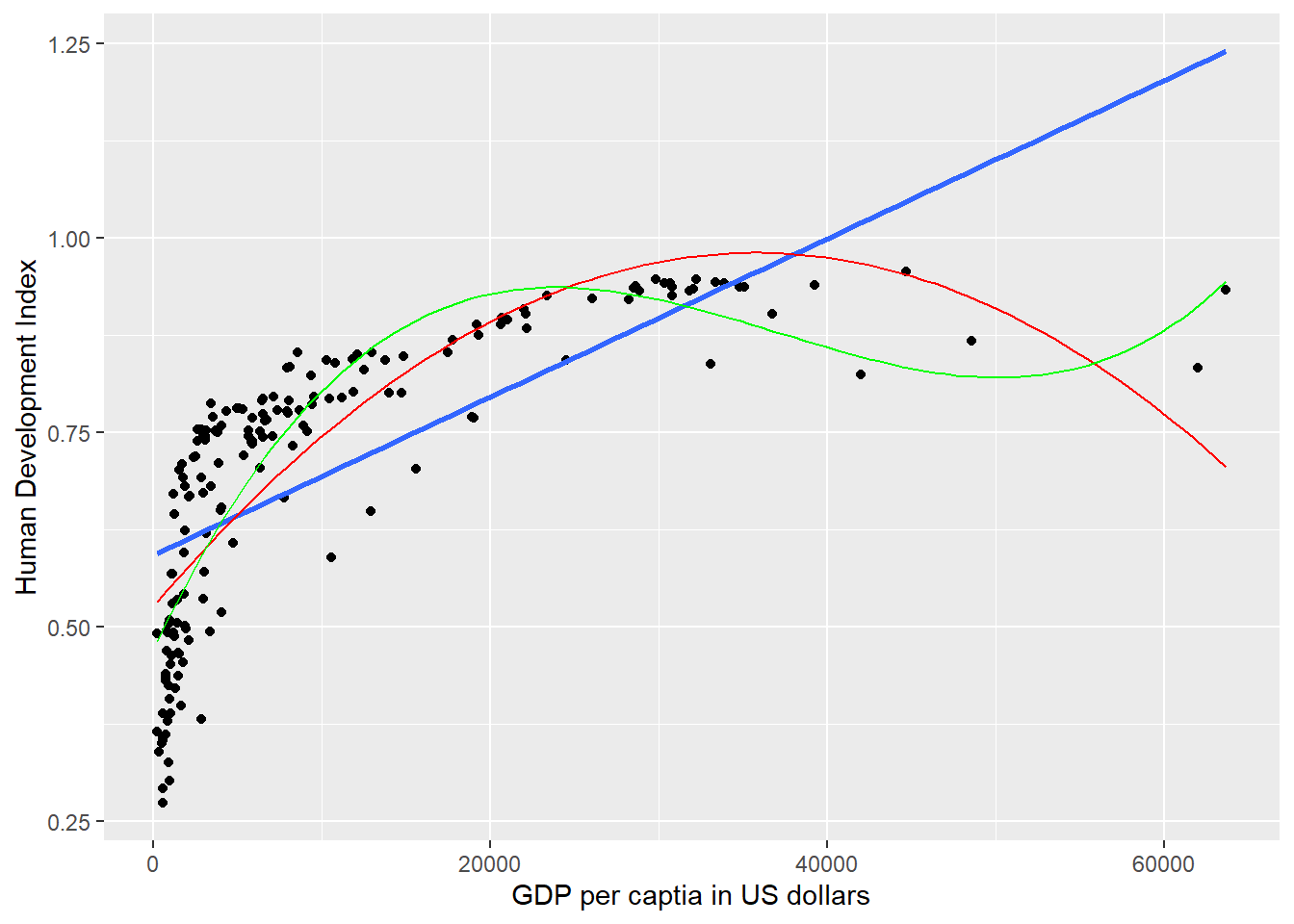

We generate an even better fit with the cubic, however it still looks somewhat strange. The cubic is being wagged around by its tail. The few extreme values cause the strange shape. This is a common problem with polynomials. We move on to an alternative.

6.1.5.2 Log-transformations

Many non-linear relationships actually do look linear on the log scale. We can illustrate this by taking the natural logarithm of GDP/captia and plot the relationship between quality of life and our transformed GDP variable.

Note: Some of you will remember from your school calculators that you have an ln button and a log button where ln takes the natural logarithm and log takes the logarithm with base 10. The natural logarithm represents relations that occur frequently in the world and R takes the natural logarithm with the log() function by default.

Below, we plot the same plot from before but we wrap gdp_capita in the log() function which log-transforms the variable.

# the scatterplot
gg_hdi_wealth_log <- ggplot(data = qog,
                            mapping = aes(x = log(wdi_gdpc),
                                          y = undp_hdi)) +
  geom_point() +
  labs(x = "GDP per captia in US dollars",
       y = "Human Development Index") 

gg_hdi_wealth_log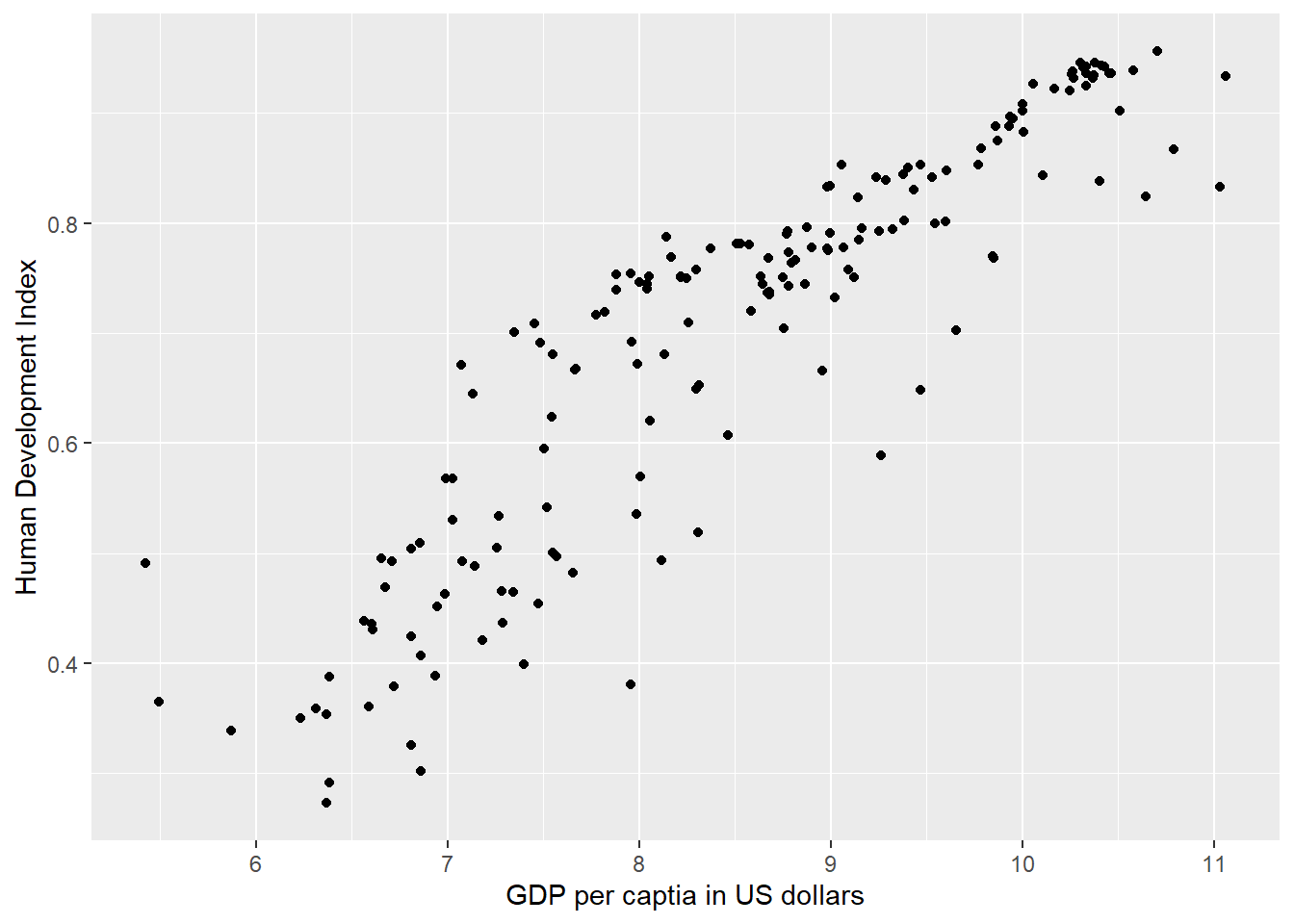

As you can see, the relationship now looks linear and we get the best fit to the data if we run our model with log-transformed gdp.

# run model with log-transformed gdp
best_model <- lm(undp_hdi ~ log(wdi_gdpc), data = qog)

# let's check our model
screenreg(list(bad_model, better_model, even_better_model, best_model),
          custom.model.names = c("Bad Model", "Better Model", "Even Better Model", "Best Model"))


===========================================================================
                    Bad Model   Better Model  Even Better Model  Best Model
---------------------------------------------------------------------------
(Intercept)           0.59 ***    0.70 ***      0.70 ***          -0.36 ***
                     (0.01)      (0.01)        (0.01)             (0.04)   
wdi_gdpc              0.00 ***                                             
                     (0.00)                                                
poly(wdi_gdpc, 2)1                1.66 ***                                 
                                 (0.10)                                    
poly(wdi_gdpc, 2)2               -1.00 ***                                 
                                 (0.10)                                    
poly(wdi_gdpc, 3)1                              1.66 ***                   
                                               (0.09)                      
poly(wdi_gdpc, 3)2                             -1.00 ***                   
                                               (0.09)                      
poly(wdi_gdpc, 3)3                              0.65 ***                   
                                               (0.09)                      
log(wdi_gdpc)                                                      0.12 ***
                                                                  (0.00)   
---------------------------------------------------------------------------
R^2                   0.49        0.67          0.74               0.81    
Adj. R^2              0.49        0.66          0.74               0.81    
Num. obs.           172         172           172                172       
===========================================================================
*** p < 0.001; ** p < 0.01; * p < 0.05

Polynomials can be useful for modelling non-linearities. However, for each power we add an additional parameter that needs to be estimated. This reduces the degrees of freedom. If we can get a linear relationship on the log scale, one advantage is that we lose only one degree of freedom.

Furthermore, we gain interpretability. The relationship is linear on the log scale of gdp/capita. This means we can interpret the effect of gdp/captia as: For an increase of gdp/captia by one percent, the quality of life increases by $\frac{0.12}{100}$ points on average. The effect is very large because human_development only varies from $0$ to $1$.

To assess model fit, the F test is not very helpful here because, the initial model and the log-transformed model estimate the same number of parameters (the difference in the degrees of freedom is 0). Therefore, we rely on adjusted R^2 for interpretation of model fit. It penalises for additional parameters. According to our adjusted R^2, the log-transformed model provides the best model fit.

To illustrate that this is the case, we return to our plot and show the model fit graphically. The yellow line shows our log-transformed fit. It clearly fits the data best.

# fitted values for the log model (best model)
y_hat3 <- predict(best_model, newdata = x)

# add to data
x$log_predict <- y_hat3

# plot
gg_hdi_wealth <- gg_hdi_wealth +
  geom_line(data = x,
            mapping = aes(x = gdp_seq,
                          y = log_predict),
            colour = "yellow",
            size = 2,
            alpha = 0.5)

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.
This warning is displayed once every 8 hours.
Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
generated.

gg_hdi_wealth

`geom_smooth()` using formula = 'y ~ x'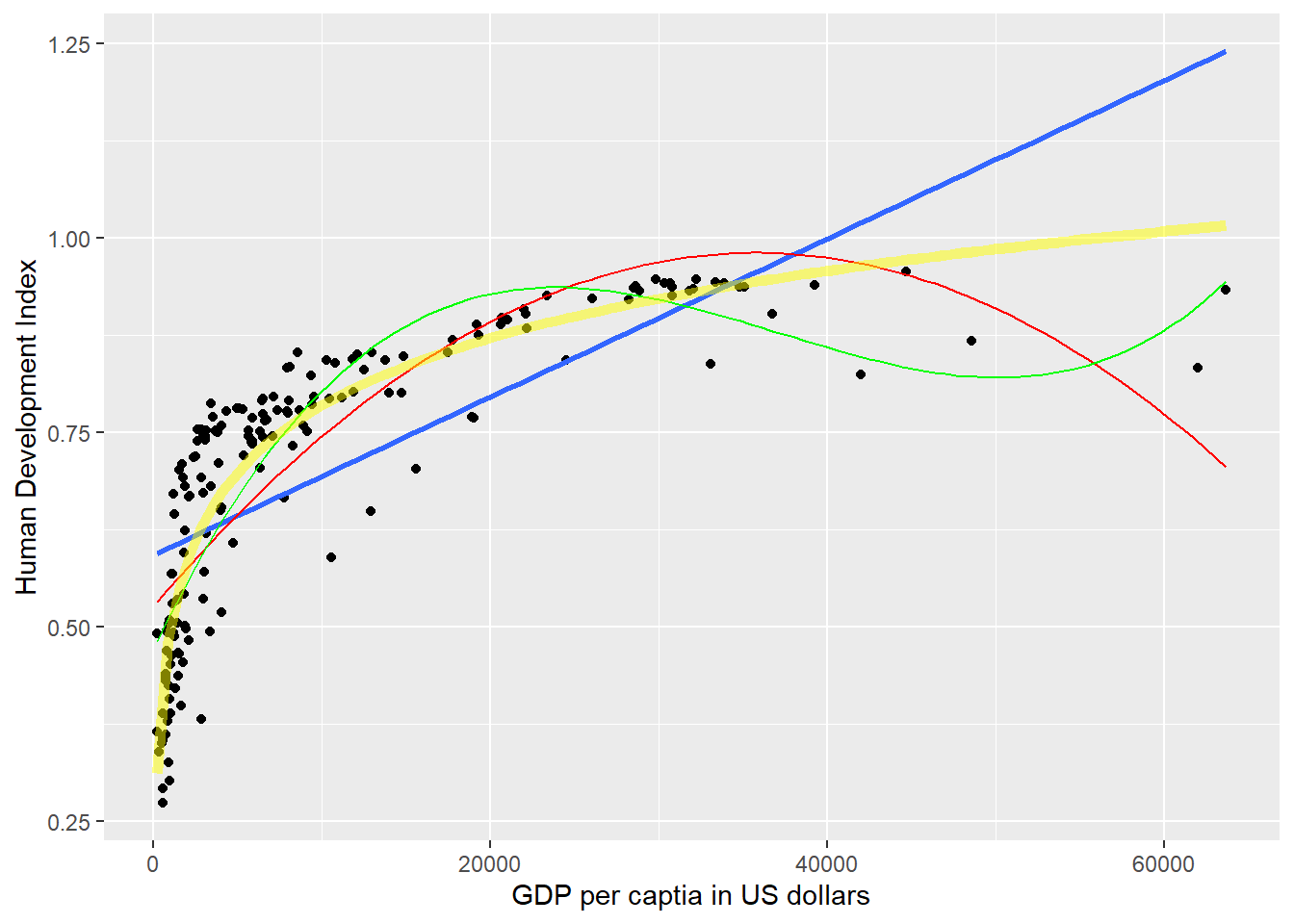

If the ggplot2 code throughout this seminar has been confusing, or you want to know more about how to use the ggplot() function for your own purposes, see Going further with the tidyverse: dplyr, magrittr and ggplot2.

6.1.5.3 Going further with intepreting interactions

An additional way to interpret your above models would be in terms of “marginal effects” that is in terms partial derivatives of continuous variables in a model.

Here we can take our above example with a quadratic transformation of GDP/capita.

# Go back to model where "square" GDP/c
better_model <- lm(undp_hdi ~ poly(wdi_gdpc, 2), data = qog)
# Automatic plot from marginaleffects::plot_slopes()
marginaleffects <- plot_slopes(better_model, variables = "wdi_gdpc", condition = "wdi_gdpc") +
  labs(x = "Per Capital GDP in USD", y = "Marginal effect of GDP/c on HDI", ) 
print(marginaleffects) # show plot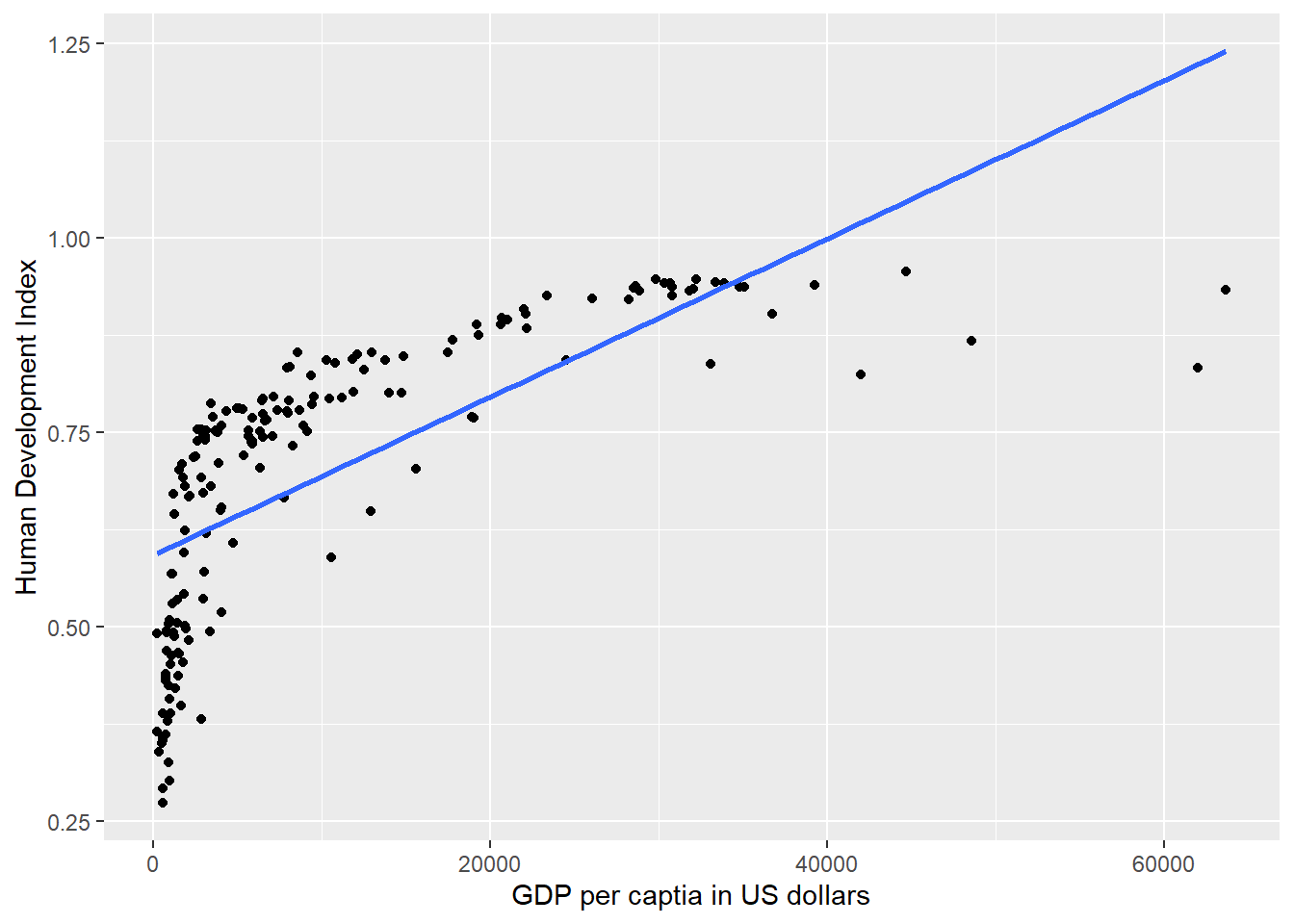

Now let us go back again and look at our plot of predicted outcomes with the quadratic term:

gg_hdi_wealth <- gg_hdi_wealth +
  geom_line(data = x,
            mapping = aes(x = gdp_seq,
                          y = prediction),
            colour = "red")

gg_hdi_wealth

`geom_smooth()` using formula = 'y ~ x'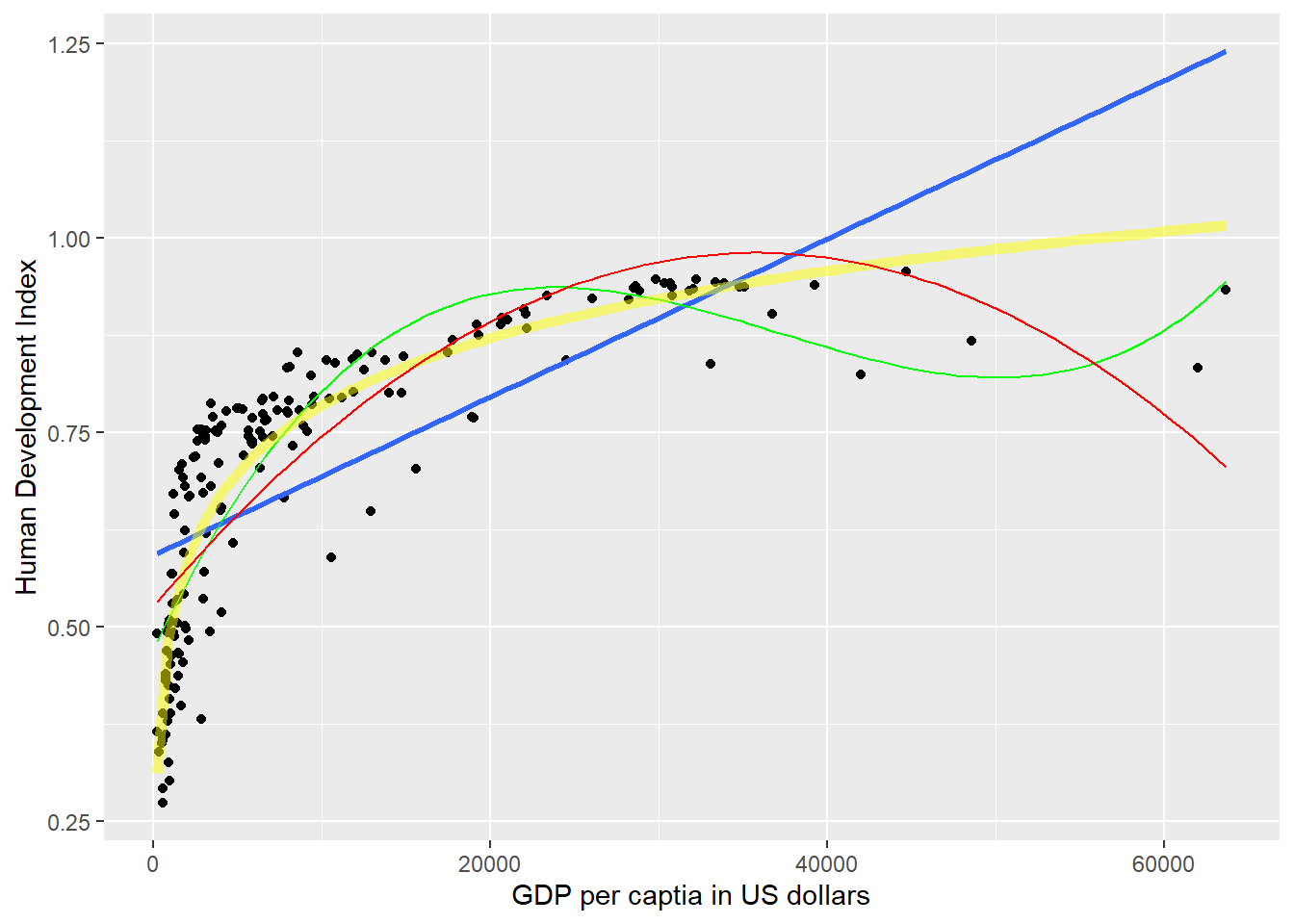

Here in red we can see the predicted level of HDI from the model with a quadratic term. We can see beyond a GPD/c of 40,000 , every increase in GDP/c reduces HDI. This corresponds to the negative predicated “marginal effects” in previous plot.

For more information on “marginal effect see the amazing blog by Andrew Heiss.

6.1.6 Homework exercises

Using better model, where we included the square of GDP/capita, what is the effect of:
1. an increase of GDP/capita from 5000 to 15000?
2. an increase of GDP/capita from 25000 to 35000?
You can see that the curve in our quadratic plot curves down when countries become very rich. Speculate whether that results make sense and what the reason for this might be.
Raise GDP/captia to the highest power using the poly() that significantly improves model fit.
1. Does your new model solve the potentially artefical down-curve for rich countries?
2. Does the new model improve upon the old model?
3. Plot the new model.
Run a model on the human development index (hdi), interacting an independent judiciary (h_j) and institutions_quality. What is the effect of quality of institutions:
1. In countries without an independent judiciary?
2. When there is an independent judiciary?
3. Illustrate your results.
4. Does the interaction improve model fit?

Ex Colony	Intercept	Slope
0 = never colony	\(\beta_0\) \(= 0.79\)	\(\beta_1\) \(= 0.08\)
1 = ex colony	\(\beta_0 + \beta_2\) = \(0.79 + -0.12 = 0.67\)	\(\beta_1 + \beta_3\) \(= 0.08 + 0.05 = 0.13\)